Making the rounds on Twitter today is a post by Ravi Parikh entitled “How to lie with data visualization.” It falls neatly into the “how to lie with statistics” genre because data visualization is nothing more than the visual representation of numerical information.
At least one graph provided by Parikh does seem like a deliberate attempt to obfuscate information–i.e., to lie:
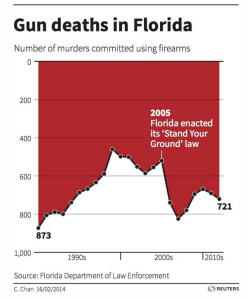
Inverting the y-axis so that zero starts at the top is very bad form, as Parikh rightly notes. It is especially bad form given that this graph delivers information about a politically sensitive subject (firearm homicides before and after the enacting of Stand Your Ground legislation).
Other graphs Parikh provides don’t seem like deliberate obfuscations so much as exercises in stupidity:
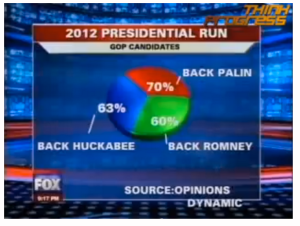
Pie charts whose divisions are broken down by % need to add up to 100%. No one in Fox Chicago’s newsroom knows how to add. WTF Visualizations—a great site—provides many examples of pie charts like this one.
So, yes, data visualizations can be deliberately misleading; they can be carelessly designed and therefore uninformative. These are problems with visualization proper, and may or may not reflect problems with the numerical data itself or the methods used to collect the data.
However, one of Parikh’s “visual lies” is more complicated: the truncated y-axis:
About these graphs, Parikh writes the following;
One of the easiest ways to misrepresent your data is by messing with the y-axis of a bar graph, line graph, or scatter plot. In most cases, the y-axis ranges from 0 to a maximum value that encompasses the range of the data. However, sometimes we change the range to better highlight the differences. Taken to an extreme, this technique can make differences in data seem much larger than they are.
Truncating the y-axis “can make differences in data seem much larger than they are.” Whether or not differences in data are large or small, however, depends entirely on the context of the data. We can’t know, one way or the other, if a difference of .001% is a major or insignificant difference unless we have some knowledge of the field for which that statistic was compiled.
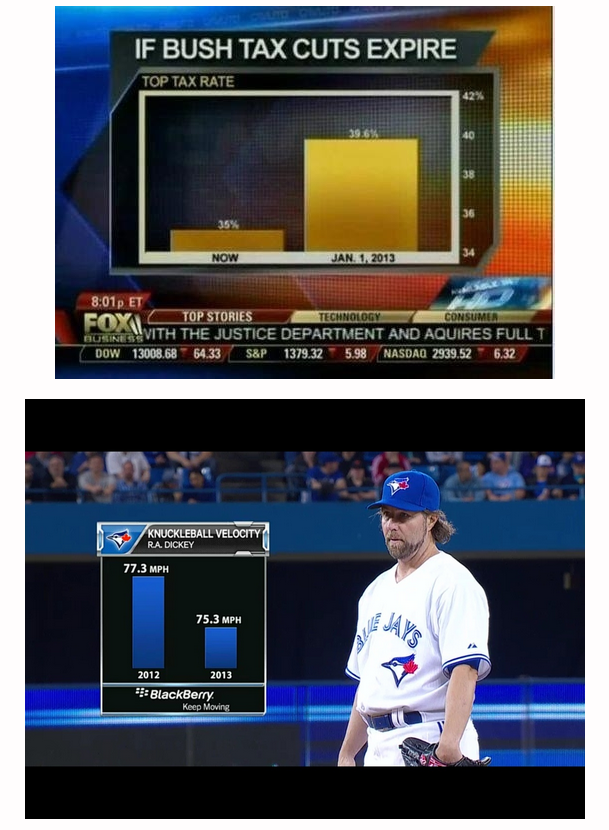
Take the Bush Tax Cut graph above. This graph visualizes a tax raise for those in the top bracket, from a 35% rate to a 39.6% rate. This difference is put into a graph with a y-axis that extends from 34 – 42%, which makes the difference seem quite significant. However, if we put this difference into a graph with a y-axis that extends from 0 – 40%—the range of income tax rates—the difference seems much less significant:
So which graph is more accurate? The one with a truncated y-axis or the one without it? The one in which the percentage difference seems significant or the one in which it seems insignificant?
Here’s where context-specific knowledge becomes vital. What is actually being measured here? Taxes on income. Is a 35% tax on income really that much greater than a 39.6% tax? According to the current U.S. tax code, this highest bracket affects individual earnings over $400,000/year and, for married couples, earnings over $450,000/year. Let’s go with the single rate. Let’s say someone makes $800,000 per year in income, meaning that $400,000 of that income will be taxed at the highest rate:
35% of 400,000 = 0.35(400,000) = 140,000
39.6% of 400,000 = 0.396(400,000) = 158,400
158,400 – 140,000 = 18,400
So, in real numbers, not percent, the tax rate hike will equal $18,400 to someone making 800k each year. It would equal more $$$ for those earning over a million. So, the question posed a moment ago (which graph is more accurate?) can also be posed in the following way: is an extra eighteen grand lost annually to taxes a significant or insignificant amount?
And this of course is a subjective question. Ravi Parikh thinks it’s not a significant difference, which is why he used the truncated graph as an example in a post titled “How to lie with data visualization.” (And as a graduate student, my response is also, “Boo-freaking-hoo.”) However, imagine a wealthy couple, owners of a successful car dealership, being taxed at this rate (based on a combined income of ~800k). They have four kids. Over 18 years, the money lost to this tax raise will equal what could have been college tuition for two of their kids. I believe they would think the difference between 35% and 39.6% is significant. (Note that the “semi-rich” favor Republicans, while the super rich, the 1%, favor Democrats.)
What about the baseball graph? It shows a pitcher’s average knuckleball speed from one year to the next. When measuring pitch speed, how significant is the difference between 77.3 mph and 75.3 mph? Is the truncated y-axis making a minor change more significant than it really is? As averages across an entire season, a drop in 2 mph does seem pretty significant to me. If Dickey were a fastball pitcher, averaging between 92 mph and 90 mph would mean fewer pitches under 90mph, which could lead to a higher ERA, fewer starts, and a truncated career. For young pitchers being scouted, the difference between an 84 mph pitch and an 86 mph pitch can apparently mean the difference between getting signed and not getting signed. Granted, there are very few knuckleballers in baseball, so whether or not this average difference is significant in the context of the knuckleball is difficult to ascertain. However, in the context of baseball more generally, a 2 mph average decline in pitch speed is worth visualizing as a notable decline.
So, do truncated y-axes qualify as the same sort of data-viz problem as pie charts that don’t add up to 100%? It depends on the context. And there are plenty of contexts in which tiny differences are in fact significant. In these contexts, not truncating the y-axis would mean creating a misleading visualization.


Pingback: How to be Honest with Data – Nerd on the Bus
no
Pingback: Makeover Monday: Chicago Taxi Journeys – Clare L. Gibson
So it seems like, by your own admission, showing a truncated graph of tax rates does not show the complete picture. In fact, you had to do more analysis in order make any point at all. You created new data. If you wanted to accurately make the point that 5.6% is a significant increase, why not plot out the relative impact in dollars of a 34% vs 39.6% marginal tax rate based on income? It looks like the bar chart is the wrong visual to use altogether in this case.
By futzing with the axis, you’re injecting opinion that otherwise would not be there and using a graph as a rhetorical trick to give your argument weight. You’re presenting your opinion in a medium generally reserved for facts. It’s just disingenuous. Hell, since you’ve already started, why not make the axis start at 33.9%? Or 33.99%? Just shift the axis until it looks like how it feels to you… would you still find that intellectually honest?
You need to re-read the post, bro, and this time, don’t confuse your own internal interjections for what’s actually on the page.
oh hey! have no idea why i wanted to look up this post again, but i did! Your response is not an argument, so I’m disappointed. “internal interjections”…i’m guessing is poorly-worded snark for “interpretations”…if I misinterpreted what you said, please clarify.
My question still stands, if your point is to demonstrate that 5.6% is a lot, why not plot your arithmetic rather than feeling out where to put the y-axis?
Your income tax example is misleading in itself. You ask “is an extra eighteen grand lost annually to taxes a significant or insignificant amount”? Well, the easiest way to answer it is to first ask “what percent of the income is that increased amount”?
18,400/800,000 = 2.3%
The fairer question is now “is the extra 2.3% significant”? It may or may not be, but at least we’re now pondering the right question.
Raw numbers and percentages are equally valuable to just about any discussion, so thanks for adding the latter. But I don’t see how adding it makes the question any less or more “misleading.” Turning raw numbers into a percentage or a percentage into raw numbers doesn’t make a question easier or more difficult to answer. It just offers a different perspective. Which one is the better perspective is, again, another subjective question.